SEISMIC DATA PROCESSING IS OUR BUSINESS

MSSA

Multichannel Singular Spectrum Analysis (MSSA) is a powerful noise attenuation technology that exploits the spatial redundancy of data. Incoherent noise is attenuated by thresholding the singular values of data embedded in structured matrices. MSSA can be applied in a variety of domains (including common source gathers, common receiver gathers, post stack volumes, common offset vectors, and cross-spreads), using up to five dimensions. Our implementation of MSSA can optionally use a statistical analysis of the singular values at all times, positions, and frequencies in a survey to optimally discriminate between signal and noise. MSSA is well suited for strong noise environments and regularly achieves a high level of signal preservation. With MSSA we are able to target a variety of noise types including random noise, high amplitude spikes, harmonics, as well as high amplitude, high frequency scattered energy.

The preservation of weak diffracted energy is often problematic during noise attenuation. MSSA is able to better preserve these events while attenuating noise. Figure 1a shows a stacked dataset containing high frequency noise overlaying weak diffractions. The results of applying MSSA are shown in figure 1b (with difference shown in figure 1c). Time slice displays (shown in figures 2a-2c) show the power of MSSA to reveal weak underlying diffractions.

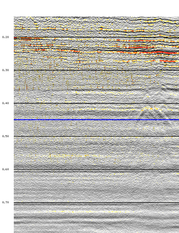
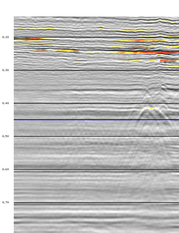
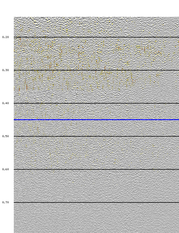
fig. 1a - Input stack with high frequency noise overlaying weak diffractions fig. 1b - Results of applying MSSA fig. 1c - Difference
Figure 1. Post-stack MSSA is able to preserve diffractions while attenuating noise.

fig. 2a - Time slice before MSSA fig. 2b - Results of applying MSSA fig. 2c - Difference
Figure 2. Time slice of data from Figure 1.