Q COMPENSATION
Q attenuation is the absorption of energy by the earth (conversion of acoustic to thermal energy). This frequency dependent loss is determined by a dimensionless quantity, Q, which describes the ratio of retained energy to lost energy over a single wavelength. Hence, small values of Q correspond to large amounts of attenuation, whereas no attenuation corresponds to an infinite Q. Typical values are between 20 and 100. The effect of Q is not only amplitude loss, but also dispersion, with low frequencies propagating slower than high frequencies. This is a necessary consequence of causality: a theory of Q which ignores dispersion would lead to energy arriving before physically possible. The relationship between the attenuation effect and the dispersion is through a Hilbert transform. One form of the equation describing attenuation and dispersion at a distance x, as a function of initial amplitude, A0, velocity c, and angular frequency ω is the following:
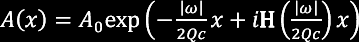
In this equation H is the Hilbert transform function.
The effect of this Q attenuation increases both with distance (or traveltime) and with frequency. The phase effect can cause difficulties tying well synthetics to the seismic.
Q compensation can be either full (accounting for amplitude and phase effects) or it can be phase only. Full compensation restores amplitudes for high frequencies in the data, and so serves to flatten the spectrum. Phase only does not change the amplitude spectrum, but will seek to restore the phase which would have been obtained in the absence of Q attenuation.
For full Q compensation, an important consideration is the presence of random noise which contaminates seismic data. Q absorption causes the attenuated signal to drop below the noise level. Q compensation can then lead to high frequency noise in the data “blowing up” and obscuring the signal. At Key Seismic we have implemented a full Q compensation based on the method of Wang (2006). This method stabilizes the Q filter by constructing a forward filter and using a regularized inversion of this to prevent noise gain. We have found this to be more effective than other common forms of Q gain control such as clipping.
We also offer the option to apply phase only Q compensation, which doesn’t require the stabilization step.
Reference
Wang, Y., 2006, Inverse Q-filter for seismic resolution enhancement: Geophysics, 71, no. 3, V51-V60

