SLIP-SWEEP NOISE REMOVAL
In the slip-sweep acquisition method, successive Vibroseis sweeps are delayed by a time which is shorter than the total sweep, but sufficient to allow for an appropriate “listen” time corresponding to the trace length after correlation. The idea is that the fundamental generated by the sweep will only contribute to signal on the intended shot record after correlation. While this is true, the actual ground force generated by the Vibroseis contains not only the fundamental from the sweep, but also harmonic components which are related by integer multiples of frequency to the fundamental. Mathematically, the mth harmonics distortion for m>0 is given by
sm(t) = am(t)exp[2 π i(m+1)Φ(t)], (1)
where am(t) is the amplitude of the m th harmonic, and Φ(t) is the instantaneous phase of the sweep. The fundamental corresponds to s0(t) as given by equation (1).
Figure 1 shows time-frequency plots, generated using a Gabor transform method, for a series of ground force measurements at four different sweep locations, in a survey which used a non-linear sweep. In addition to the fundamental mode, labelled s0, we have identified the first and second harmonics, s1 and s2, respectively. Seven or eight different harmonics are clearly visible at each location.
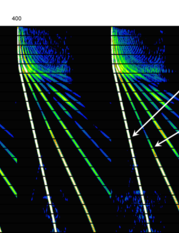
Figure 1. Time-frequency analysis of the ground force at every 10th shot, using a Gabor transform. Note the variability of the harmonic response and noise.
These same harmonics are present in the recorded trace data, but convolved with the earth response. Because the harmonics occur at the same time as the fundamental, but with higher frequency, they are propagated into times prior to the current record when correlation is performed. This leads to contamination of earlier shot records by the harmonics on later shot records. Typically slip-sweep Vibroseis records are acquired in groups of 2, 3 or 4 sweeps. In these groups, the last record will be uncontaminated, but earlier ones will contain harmonic contamination.
Figure 2 shows this effect on two shots from a slip-sweep survey. Shot 65 follows shot 64 with a slip time of just over 6 seconds. Shot 65 is itself uncontaminated, but shot 64 displays harmonic contamination from shot 65.
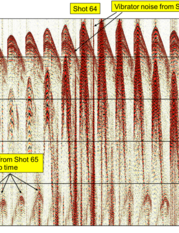
Figure 2a. Shot 64 showing harmonic contamination.
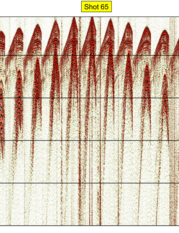
Figure 2b. Shot 65 uncontaminated by harmonic distortion.
Harmonic Noise Removal
Key has developed the CHARM process (Cleaning HARMonic noise) to predict and then subtract the harmonic noise, based upon the relationship between the ideal sweep and the measured ground force. An example of using CHARM to remove harmonic noise from a typical slip-sweep record is shown in Figure 3. The first image is the contaminated record, due to harmonics generated by a subsequent shot. The second image shows the same record after removal of the harmonic noise. The third image is the difference or noise removed during the process. It is clear that the noise originates from a shot with a different spatial location from the current shot.


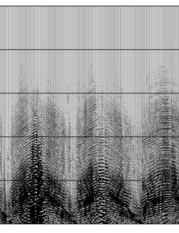
Figure 3. CHARM applied to a contaminated slip-sweep record.

